势能分析法

发表于 更新于 分类于
势能分析法的简单讲解及应用。

概述

大致思想

势能法摊借用了物理学中的概念，还分析将数据结构中的预付代价表示为“势能”，将积攒的势能释放可以支付未来操作的代价，将势能与整个数据结构相关联。

定义

对于一个初始数据结构 \(D_0\)，我们将执行 \(n\) 个操作，\(\forall i\in[1,n]\)，定义 \(c_i\) 表示此次操作所花费的实际代价，\(D_i\) 表示在 \(D_{i-1}\) 的基础上执行第 \(i\) 个操作后的结果数据结构。定义势函数 \(\Phi\) 将每个数据结构 \(D_i\) 映射到一个实数 \(\Phi(D_i)\)，表示数据结构 \(D_i\) 的势能。第 \(i\) 个操作的摊还代价 \(\hat c_i\) 用势函数 \(\Phi\) 定义为： \[ \hat c_i=c_i+\Phi(D_i)-\Phi(D_{i-1}), \] 于是，\(n\) 个操作的总摊还代价为 \[ \sum\limits_{i=1}^n\hat c_i=\sum\limits_{i=1}^n(c_i+\Phi(D_i)-\Phi(D_{i-1}))=\sum\limits_{i=1}^nc_i+\Phi(D_n)-\Phi(D_0). \] 此时，如果能定义一个势函数 \(\Phi\)，使得 \(\Phi(D_n)\geq\Phi(D_0)\)，那么显然此时总摊还代价 \(\sum\limits_{i=1}^n\hat c_i\) 就是总实际代价的一个上界。

简单理解

可以有这样一种简单的理解方式：对于 \(\Phi(D_i)-\Phi(D_{i-1})>0\)，这时这个操作正在花费额外的代价积累势能，反之，若 \(\Phi(D_i)-\Phi(D_{i-1})<0\) 则意味着正在消耗之前积累的势能进行操作，免去了一些代价。

在算法、数据结构的实际使用过程中，我们并不总能知道我们要进行多少个操作，于是，如果我们能够保证有 \(\forall i,\Phi(D_i)\geq\Phi(D_0)\)，就能保证不论多少个操作，最终得到的总摊还代价总是总实际代价的一个上界，也就是保证了所有消耗势能的操作所消耗的势能都已经在其之前通过某些操作被积累。

显然此时得到的摊还代价取决于我们定义的势函数，但是不论采用的势函数是怎样的，得到的摊还代价总是实际代价的一个上界。在选择势函数时，我们需要考虑我们需要怎样的时间界。

例题

栈问题

栈有 \(\text{POP}\)、\(\text{PUSH}\) 和 \(\text{MULTIPOP}\) 三种操作，分别是弹出栈顶，压入栈，批量弹出。压入、弹出单个元素的单次时间复杂度为 \(O(1)\)，我们假定其为 \(1\)。我们将栈的势函数定义为在其中的元素数量，对于初始的空栈，有 \(\Phi(D_0)=0\)，显然栈中元素的个数不会少于 \(0\) 个，于是必然有 \[ \Phi(D_i)\geq0=\Phi(D_0), \] 于是，我们此时用 \(\Phi\) 定义的总摊还代价是总实际代价的一个上界。我们下面对栈的三个操作分别进行摊还代价分析。

假设第 \(i\) 个操作是 \(\text{PUSH}\)，有 \[ \hat c_i=c_i+\Phi(D_i)-\Phi(D_{i-1})=1+1=2, \] 假设第 \(i\) 个操作是 \(\text{POP}\)，有 \[ \hat c_i=c_i+\Phi(D_i)-\Phi(D_{i-1})=1-1=0, \] 假设第 \(i\) 个操作是 \(\text{MULTIPOP}(k)\)，此时栈中有 \(s\) 个元素，那么将弹出 \(k'=\min(k,s)\) 个元素，于是有 \[ \hat c_i=c_i+\Phi(D_i)-\Phi(D_{i-1})=k'-k'=0, \] 综上，每个操作的摊还代价都是 \(O(1)\)，于是 \(n\) 个操作的总摊还代价应当为 \(O(n)\)，此时是总实际代价的上界，于是最坏情况下的总实际代价为 \(O(n)\).

动态扩增数组问题

给定一个数组，其初始大小为 \(0\)，支持在数组末尾加入一个元素；如果当前大小为 \(0\)，则先开 \(1\) 的空间，如果数组元素已满，则先将数组的大小翻倍再插入，开单个空间和插入一个元素的时间视为 \(1\)。求操作的平摊复杂度。

容易发现，造成复杂度分析困难的一步是开新空间时的时间复杂度，开新数组时的耗时巨大，但实际进行的操作次数并不多，于是我们希望这一步在分析时能够采用积累的势能进行，也就是说，我们希望这是一个消耗势能的操作。

于是我们希望定义的势函数能够使得当前处于已满状态的数组的势能最大，为数组的规模，在刚新开完空间后的势能为 \(0\)，我们这样定义 \(\Phi\): \[ \Phi(D_i)=2\cdot num_i-size_i, \] 其中 \(num_i\) 当前数组存储的元素个数，而 \(size_i\) 为当前数组的规模，显然，这样定义能够满足我们的要求。

在初始空数组时，其势能为 \(0\)，而根据上面描述的数组扩增的算法，显然在任意时刻，数组内元素个数至少为表规模的一半，于是在任意时刻都有 \(\Phi(D_i)\geq 0=\Phi(D_0)\)，也就意味着最终可以得到一个实际总代价的上界。

我们将所有的插入操作分为两种进行讨论：引起了数组扩张与未引起数组扩张。下面用 \(\varphi_i\) 表示 \(\Phi(D_i)\).

未引起数组扩张时，有 \(num_{i-1}=num_i-1, size_i=size_{i-1}\)，于是有： \[ \begin{aligned} \hat c_i&=c_i+\varphi_i-\varphi_{i-1}\\ &=1+(2\cdot num_i-size_i) - (2\cdot num_{i-1}-size_{i-1})\\ &=1+2\cdot(num_i-num_{i-1})=1+2=3 \end{aligned} \] 当引起了数组扩张时，首先有一个特例：开始时的第一次插入引起了表扩张，此时是积累势能： \[ \begin{aligned} \hat c_1&=c_1+\varphi_1-\varphi_{0}\\ &=1+(2\cdot num_1-size_1) - (2\cdot num_{0}-size_{0})\\ &=1+1-0=2 \end{aligned} \] 其余的引起表扩张的情况，一定有 \(num_i-1=num_{i-1}=size_{i-1}, size_i=2\cdot size_{i-1}\)，于是有： \[ \begin{aligned} \hat c_i&=c_i+\varphi_i-\varphi_{i-1}\\ &=num_{i-1}+1+(2\cdot num_i-size_i) - (2\cdot num_{i-1}-size_{i-1})\\ &=num_i+(2\cdot num_i-2\cdot (num_i - 1))-(2\cdot(num_i - 1)-(num_i-1))\\ &=num_i+2-(num_i-1)=3 \end{aligned} \] 于是综上所述，每个操作的摊还代价是 \(O(1)\)， \(n\) 个操作的总摊还代价就是 \(O(n)\).

伸展树(Splay)的时间复杂度分析

Splay 的各种操作的核心就是 splay() 操作，其余的只是常数上的变化。

记 \(x\) 表示一棵有 \(n\) 个点的 Splay 上的一个节点，\(x'\) 表示操作后的对应节点，\(|x|\) 表示 Splay 上 \(x\) 的子树大小。一次旋转的时间复杂度为 \(O(1)\)，这里视为 \(1\)。我们希望用势能函数的变化量抵消掉 Splay 上节点的访问代价，定义整棵 Splay 的势函数为 \(\Phi(S)=\sum\limits_{x\in S}\varphi(x)\)，其中 \(\varphi(x)=\log|x|\).

对于访问节点带来的时间开销，我们将其均摊到旋转操作中，可以轻易地调整势函数中的常数进行抵消。

  1. 三点一线
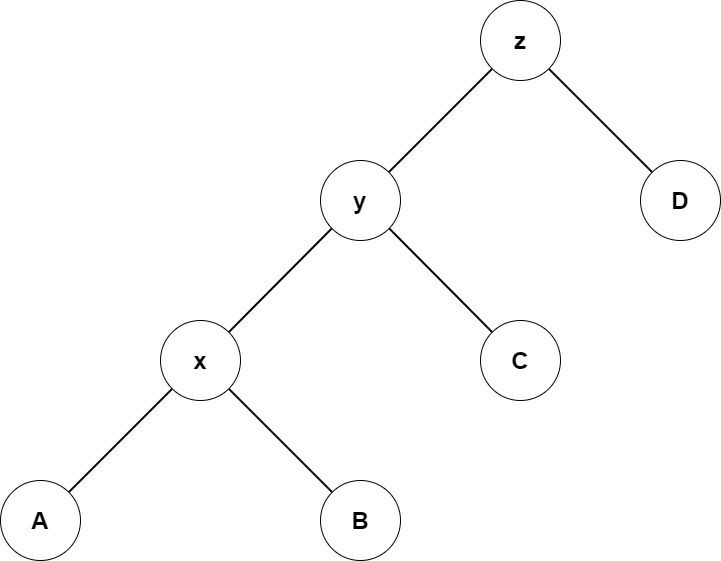
Splay_1.png
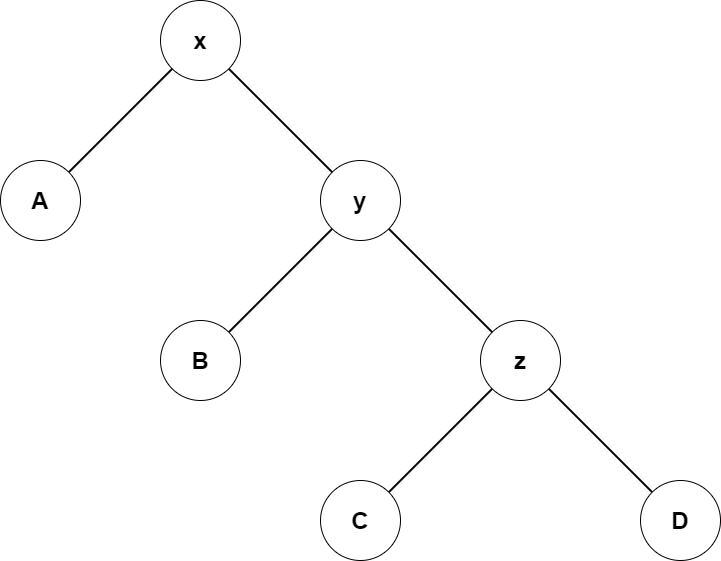
Splay_2.png

势能变化量为 \[ \begin{aligned} \Phi_i-\Phi_{i-1}=&\varphi_i(x)+\varphi_i(y)+\varphi_i(z)\\ &-\varphi_{i-1}(x)-\varphi_{i-1}(y)-\varphi_{i-1}(z)\\ \leq&\varphi_i(x)-\varphi_{i-1}(x)+\varphi_i(z)-\varphi_{i-1}(y)\\ \leq&\varphi_i(x)+\varphi_i(z)-2\cdot\varphi_{i-1}(x) \end{aligned} \] 观察上面的树，不难发现有 \[ |x'|\geq|x|+|z'|, \] 于是我们可以得到（注意式子与上面不一样） \[ \begin{aligned} &\varphi_{i-1}(x)+\varphi_{i-1}(z)-2\cdot\varphi_{i}(x)\\ =&\log\dfrac{|x||z'|}{|x'|^2}=\log\dfrac{|x||z'|}{(|x|+|z'|)^2}\\ \leq&\log\dfrac{|x||z'|}{2|x||z'|}=\log\dfrac1 2=-1 \end{aligned} \] 于是有 \[ \hat c_i=c_i+\Phi_i-\Phi_{i-1}\leq1+3\cdot(\varphi_i(x)-\varphi_{i-1}(x))-1=3\cdot(\varphi_i(x)-\varphi_{i-1}(x)). \]

  1. 三点不在同一直线
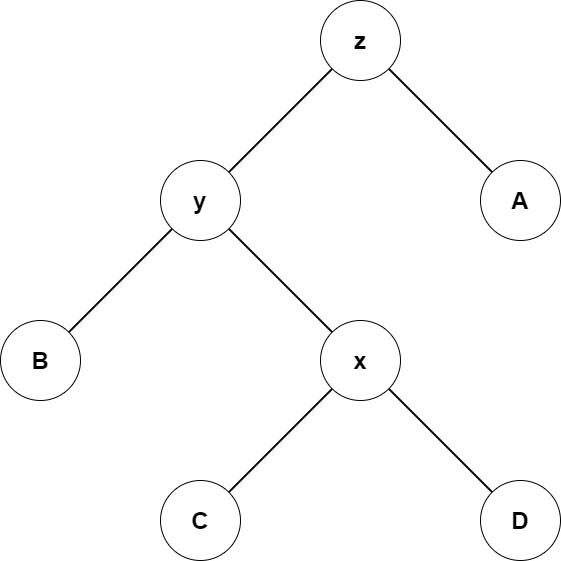
Splay_3.png
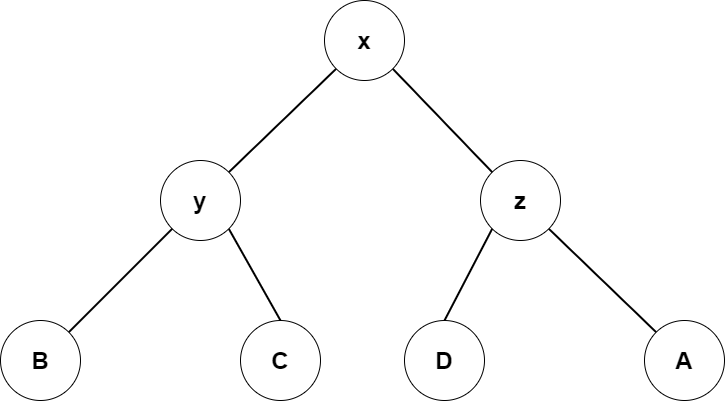
Splay_4.png

势能变化量为 \[ \begin{aligned} \Phi_i-\Phi_{i-1}=&\varphi_i(x)+\varphi_i(y)+\varphi_i(z)\\ &-\varphi_{i-1}(x)-\varphi_{i-1}(y)-\varphi_{i-1}(z)\\ =&\varphi_i(y)+\varphi_{i}(z)-\varphi_{i-1}(x)-\varphi_{i-1}(y)\\ \end{aligned} \] 观察上图，我们可以得到 \[ |y'|+|z'|\leq|x'| \] 同理可得 \[ \varphi_i(y)+\varphi_i(z)-2\cdot\varphi_{i}(x)\leq-1 \] 于是有 \[ \begin{aligned} \hat c_i=&c_i+\Phi_i-\Phi_{i-1}\\ \leq&\varphi_i(y)+\varphi_{i}(z)-\varphi_{i-1}(x)-\varphi_{i-1}(y)\\ &-(\varphi_i(y)+\varphi_i(z)-2\cdot\varphi_{i}(x))\\ =&2\cdot \varphi_i(x)-\varphi_{i-1}(x)-\varphi_{i-1}(y)\\ \leq&2\cdot(\varphi_i(x)-\varphi_{i-1}(x)) \end{aligned} \]

  1. 单次旋转到根

\[ \hat c_i=c_i+\Phi_i-\Phi_{i-1}=1+\varphi_i(x)-\varphi_{i-1}(x) \]

综上，1. 2. 两种情况的摊还代价就是 \(O(\varphi_i(x)-\varphi_{i-1}(x))\)，3. 的摊还代价是 \(O(1+\varphi_i(x)-\varphi_{i-1}(x))\)，一次 splay() 操作就是若干次 1. 2. 与至多一次 3. 的结合，于是单次 spaly 操作的总摊还代价应当是 \(O(1+\varphi_{k}(x)-\varphi_0(x))\leq O(1+\log n)=O(\log n)\).

由于其他操作都基于 splay() 操作，额外消耗的仅是常数复杂度，可以直接在势函数中用常数平衡，于是一棵 Splay 的各种操作的时间复杂度都可以看作 \(O(\log n)\)，将文章开始定义中的式子稍作变形可以得到 \[ \sum\limits_{i=1}^nc_i=\sum\limits_{i=1}^n\hat c_i+\Phi(D_0)-\Phi(D_n) \] 根据上面的分析，\(m\) 次操作的总摊还复杂度为 \[ \sum\limits_{i=1}^n\hat c_i=O(m\log n) \] 根据这里势函数的定义，有 \[ -n\log n\leq \Phi(D_0)-\Phi(D_m)\leq n\log n \] 于是有 \[ \begin{aligned} \sum\limits_{i=1}^nc_i=&\sum\limits_{i=1}^n\hat c_i+\Phi(D_0)-\Phi(D_m)\\ \leq&O(m\log n) +n\log n\\ =&O((m+n)\log n) \end{aligned} \]

LCT 的所有操作都以 Access() 为基础，同时这也是所有函数的核心，其他部分的复杂度都是常数。

这里将 Access() 操作分成两部分：在实链 Splay 上、转变实虚链。

  1. 在实链 Splay 上

主要的复杂度只是 splay() 操作，与上文同样的分析方式，容易得到总的复杂度为 \(O((n+m)\log n)\).

  1. 转变实虚边

采用轻重链剖分，将子树最大的儿子作为重儿子，将虚边分为重虚边与轻虚边，实边以此类推。定义势函数 \(\Phi\) 为重虚边的数量。

Access() 过程中有以下两种变化可能：

  • 势能增加 \(1\)，当且仅当选择的实边由重边切换到了轻边，根据轻重链剖分重链的性质，一次 Access()过程中此过程不超过 \(\log n\) 次；
  • 势能减小 \(1\)，当且仅当选择的实边由轻边切换到了重边；

设 \(\sum\Delta\Phi^+\) 表示所有正势能变化量的和，\(\sum\Delta\Phi^-\) 表示所有负的势能变化量的和，显然有 \[ \left|\sum\Delta\Phi^-\right|\leq\Phi(S_0)+\sum\Delta\Phi^+\leq n+m\log n\tag1 \] 于是势能变化总量为 \[ \Phi(S_{m})-\Phi(S_0)=\sum\Delta\Phi^-+\sum\Delta\Phi^+\leq n+m\log n \] 每次换边的时间复杂度为 \(O(1)\)，视为 \(1\)，根据定义有 \[ \sum\limits_{\Phi_i>0} c_i+\sum\limits_{\Phi_i<0} c_i\leq m\log n+\left|\sum\Delta\Phi^-\right|\leq n+2\cdot m\log n \] 于是有 \[ \begin{aligned} \sum_{i=1}^m\hat c_i=&\sum_{i=1}^m c_i+\Phi(S_{m})-\Phi(S_0)\\ \leq&2\cdot n+3\cdot m\log n\\ =&O(n+m\log n) \end{aligned} \] 综上所述，LCT 的时间复杂度为 \(O((n+m)\log n)\).

参考资料